N-Dimensional Gaussians for Fitting of High Dimensional Functions

SIGGRAPH 2024 (Conference Track)

Stavros Diolatzis1     Tobias Zirr1     Alexandr Kuznetsov1     Georgios Kopanas2, 3     Anton Kaplanyan1
1 2 3
Paper 84MB Paper 4MB Supplemental Code
Our method optimizes N-Dimensional Gaussians to approximate high dimensional anisotropic functions in a few minutes. Our parameterization, culling and optimization-controlled refinement allows us to quickly estimate Gaussian parameters to represent various complex functions. We show two applications:
  • 10D+ Application (Top): Synthetic scenes for which we can render G-Buffers such as world position, albedo, roughness etc. can be shaded with global illumination through our 10D+ Gaussian mixture. Even though the Gaussians are evaluated on the surfaces their representation power can efficiently estimate the appearance of reflections and transmittance with correct parallax effects. Apart from the G-Buffers we support variability of moving objects and light sources as extra dimensions.
  • 6D Application (Bottom): Real world scenes with complex view dependent effects can be modeled efficiently through our 6 dimensional Gaussian mixture. The 6 dimensions of world position and view direction give the parameterization the same representation power for both diffuse and view dependent effects, reconstructing complex effects like the one through the magnifying glass.

Abstract

In the wake of many new ML-inspired approaches for reconstructing and representing high-quality 3D content, recent hybrid and explicitly learned representations exhibit promising performance and quality characteristics. However, their scaling to higher dimensions is challenging, e.g. when accounting for dynamic content with respect to additional parameters such as material properties, illumination, or time. In this paper, we tackle these challenges for an explicit representations based on Gaussian mixture models. With our solutions, we arrive at efficient fitting of compact N-dimensional Gaussian mixtures and enable efficient evaluation at render time: For fast fitting and evaluation, we introduce a high-dimensional culling scheme that efficiently bounds N-D Gaussians, inspired by Locality Sensitive Hashing. For adaptive refinement yet compact representation, we introduce a loss-adaptive density control scheme that incrementally guides the use of additional capacity towards missing details. With these tools we can for the first time represent complex appearance that depends on many input dimensions beyond position or viewing angle within a compact, explicit representation optimized in minutes and rendered in milliseconds.

Method

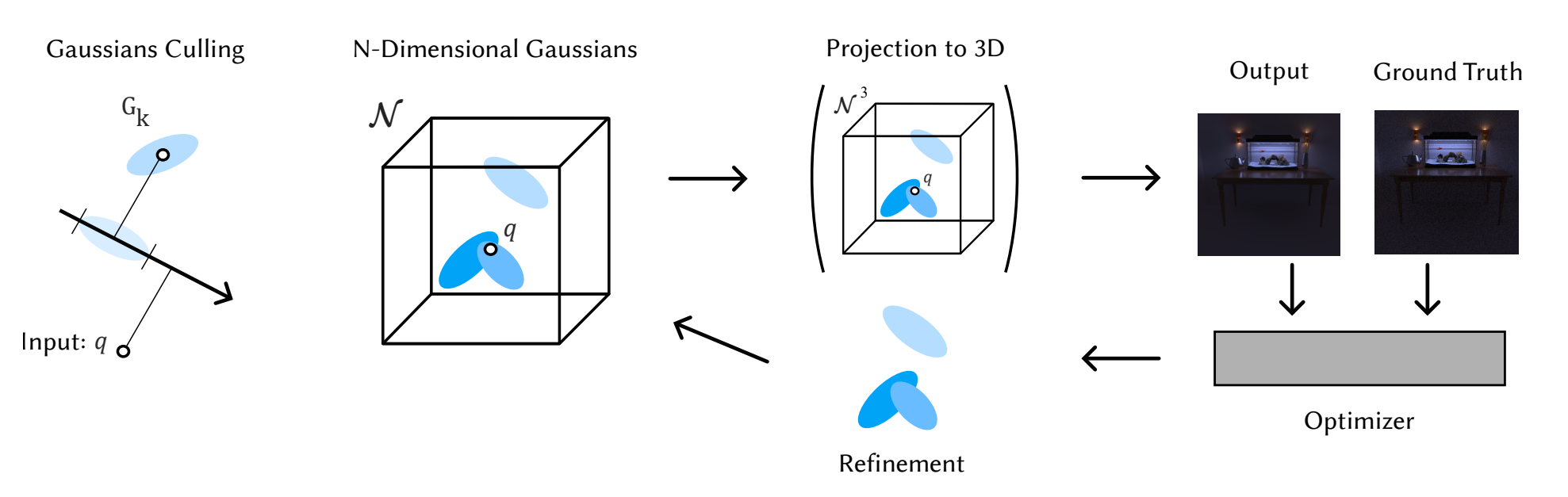
Our optimization receives a number of query points q of N dimensionality as input. For these given points we estimate which Gaussians can be discarded safely through our N-Dimensional culling inspired by Locality Sensitive Hashing. With the remaining ones we evaluate for each q our Gaussian mixture either in N dimensions for surface radiance fields or by first projecting the Gaussians to 3D. Our optimization converges to high quality while it also controlling the introduction of new Gaussians via our Optimization Controlled Refinement.

N-Dimensional Gaussians Culling

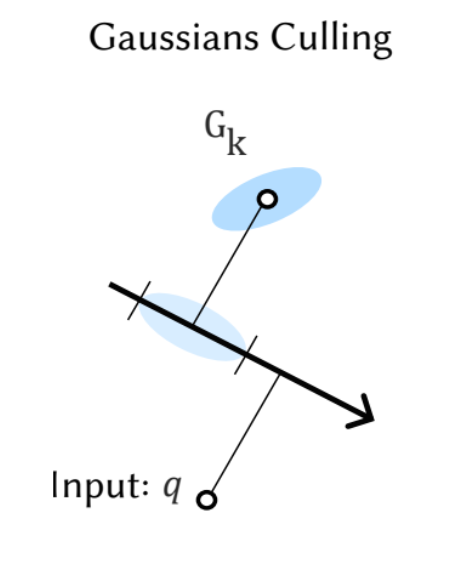
Culling irrelevant Gaussians is challenging in higher dimensions. Inspired by Locality Sensitive Hashing where locality is estimated by projection to random vectors we project both our Gaussians and the query points on random vectors and discard Gaussians safely if they fall far away from the query points. This is a tunable culling process that doesn't require any data structure and it works as the Gaussians are changing during optimization.

Optimization Controlled Refinement

In higher dimensions the refinement process of the Gaussian mixture becomes much more challenging. With many dimensions to choose from which one should we use as a criterion for refinement? Which one should we split along? To avoid this we propose a refinement process controlled by the optimizer instead. Each main Gaussian (Blue) receives two low opacity/brightness child Gaussians (Green) that are linked with the parent through a hierarchical relationship (see paper). In this way the optimizer can choose to utilize them to add details. Once these Gaussians are used enough they become main Gaussians and have child Gaussians of their own. We can see in the training video how Green Gaussians are introduced to add details.

In this training every 300 iterations we introduce new child Gaussians (Green) to the main Gaussians (Blue). As the training progress the child Gaussians add more and more fine details to the 6D Gaussian mixture without a splitting or merging mechanism.

Comparison

6D Gaussians

10D+ Gaussians

Acknowledgements

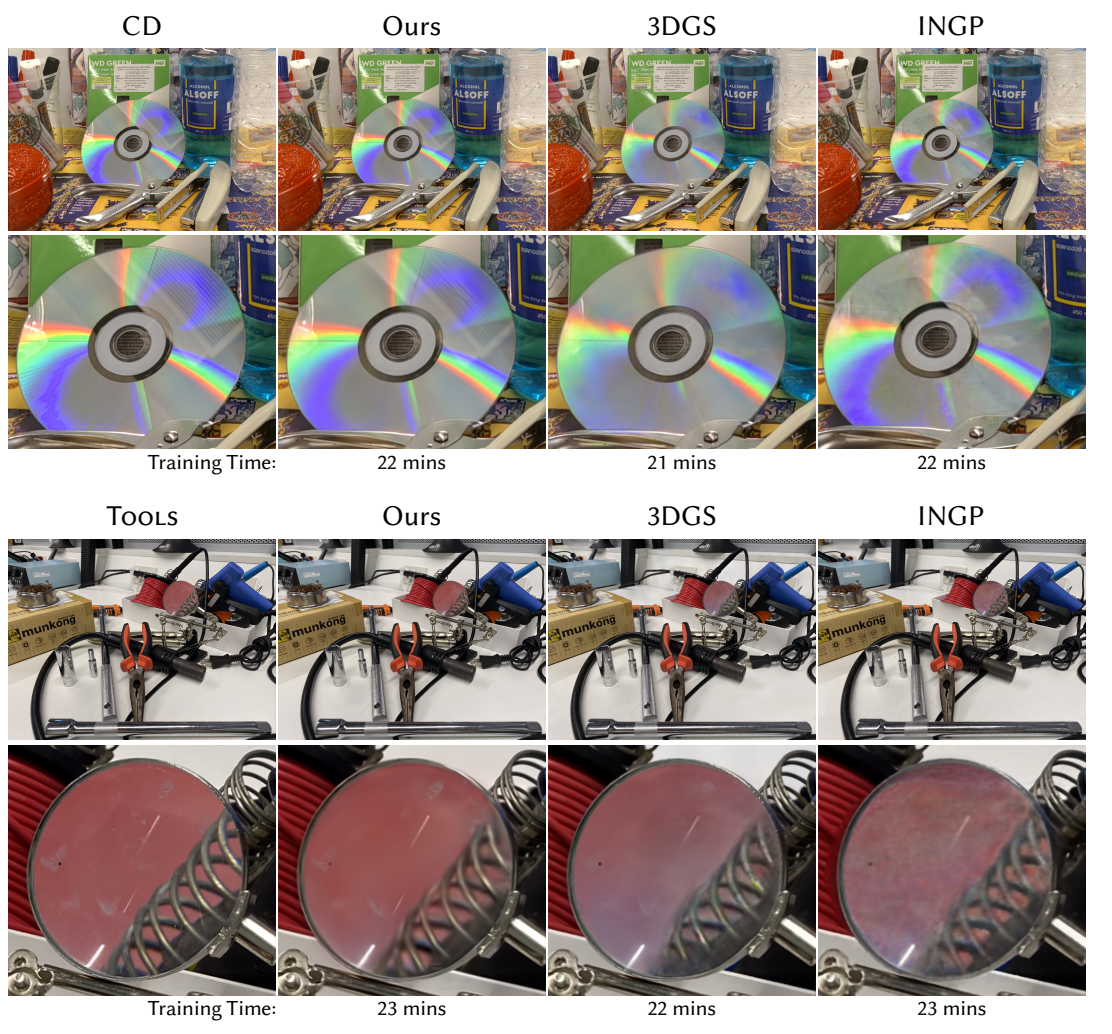
We would like to thank the anonymous referees for their valuable comments and helpful suggestions. We also thank Laurent Belcour and Sebastian Herholz for their valuable input and suggestions.

We thank the authors of Nerfies for open sourcing the webpage templated which we used for this site.